-
Welcome to Smashboards, the world's largest Super Smash Brothers community! Over 250,000 Smash Bros. fans from around the world have come to discuss these great games in over 19 million posts!
You are currently viewing our boards as a visitor. Click here to sign up right now and start on your path in the Smash community!
It appears that you are using ad block :'(
Hey, we get it. However this website is run by and for the community... and it needs ads in order to keep running.
Please disable your adblock on Smashboards, or go premium to hide all advertisements and this notice.
Alternatively, this ad may have just failed to load. Woops!
Please disable your adblock on Smashboards, or go premium to hide all advertisements and this notice.
Alternatively, this ad may have just failed to load. Woops!
Need Math Help?
- Thread starter AltF4
- Start date
Blissard
Smash Lord
+1 Asian, and +1 post as well....Can we have a head count of how many Asians are in this thread (not as an insult, as a respecct)?
metalreflectslime
Chemistry PhD Programs?
Asians
Metal Reflect Slime
Blissard
Gosu_Engineer (he has been inactive due to work lately though)
Can we have a head count of how many Asians are in this thread (not as an insult, as a respecct)?
Asians in this thread:+1 Asian, and +1 post as well....
Metal Reflect Slime
Blissard
Gosu_Engineer (he has been inactive due to work lately though)
Kason Birdman
Smash Champion
Prolly gonna come to this thread in the future for help.
Solstice
Smash Rookie
- Joined
- Sep 26, 2010
- Messages
- 20
Nature's Way makes organic cereal. They can produce up to 100,000 boxes of cereal per month at a cost of $1.20 per box. The fixed costs are $45,000 per month. Each box sells for $2.00. Due to higher demand for organic food, Nature's Way has to pay more for it ingredients. If the cost per box increased by 25% but the foxed costs are still $45,000, what must the new selling price be if they want to earn a profit of $21,000 from the sale of 60,000 boxes? If they incurred a loss of $15,000, how many boxes of cereal were produced and sold? What are total monthy sales required to break even? If their sales are $40,000 for the month, how much is their profit or loss? At what percentage capacity must they operate to break even?
Please help.
edit: spelled organic wrong lol
Please help.
edit: spelled organic wrong lol
Gosu_Engineer
Smash Ace
Orginal Cost: (production costs) + (fixed costs) = Number of boxes made*$1.20 + $45000Nature's Way makes organic cereal. They can produce up to 100,000 boxes of cereal per month at a cost of $1.20 per box. The fixed costs are $45,000 per month. Each box sells for $2.00. Due to higher demand for organic food, Nature's Way has to pay more for it ingredients. If the cost per box increased by 25% but the foxed costs are still $45,000, what must the new selling price be if they want to earn a profit of $21,000 from the sale of 60,000 boxes? If they incurred a loss of $15,000, how many boxes of cereal were produced and sold? What are total monthy sales required to break even? If their sales are $40,000 for the month, how much is their profit or loss? At what percentage capacity must they operate to break even?
Please help.
edit: spelled organic wrong lol
New costs: 1.25*(production costs) + (fixed costs) = 1.25* Number of boxes made*$1.20 + $45000
from 60000 boxes, total costs would be 1.25* (60000)*$1.20 + $45000 = $135000
Profit = Revenue - cost
from here it's just algebra Profit needs to be $21,000 and we just calculated the cost.
The Revenue is (# of boxes sold)*(unit price) = 60000*(unit price)
So we use the equation: $21,000 =60000*(unit price)
- (1.25* (60000)*$1.20 + $45000) just use algebra
I get $2.60. you probably should double check
"incurred a loss of $15,000" Means Cost exceeded revenue by that amount and profit in the previous equation would be negative:
-$15000 = Revenue - cost
Cost is 1.25* Number of boxes made*$1.20 + $45000
Revenue is # of boxes sold times the unit price which I'm assuming is the one we just calculated
-$15000 = (#)*$2.60 - (1.25*(#)*$1.20 + $45000)
# = 27273 boxes
to break even Profit equals 0
0 = (#)*$2.60 - (1.25*(#)*$1.20 + $45000)
# = 40909 boxes
To convert to a percentage divide this number by their total capacity: 40909/100000
~40.91%
Note you also spelled "fixed" incorrectly
Kinzer
Mammy
I need help with a physics question, I don't know where to start.
Each year, the Punkin' Chunkin' contest is held in Lewes, Delaware. The object is to propel an 8- to 10-pound pumpkin as far as possible. Steve Young of Hopewell, Illinois, set the 1998 world record of 4026.32 feet. Suppose you build a machine that fires the pumpkin so that it is at a height of 124 feet after one second, 272 feet after three seconds, and the height at eight seconds is 82 feet. Refer to the formula in exercise 7 to find the acceleration, the initial velocity, and the initial height of the pumpkin.
I find it strange that the teacher wants me to do a physics exercise when I'm working on Pre-Calculus, and moreso that he didn't specify that I would have to go back to an exercise he didn't say had to be done in this lesson, but for the sake of having more resources, this is what exercise 7 says:
The height of an object that is thrown upward with a constant acceleration of a feet per second per second (I swear to God it's written twice in the book) is given by the equation
s = 1/2at^2 + Vot + So
The height is s feet, t represents the time in seconds, Vo is the initial velocity in feet per second, and So is the initial height in feet. Find the acceleration, the initial velocity, and the initial height if the initial height at 1 second is 75 feet, the height at 2.5 seconds is 75 feet, and the height at 4 seconds is 3 feet.
Thank you for taking the time to look at this.
Each year, the Punkin' Chunkin' contest is held in Lewes, Delaware. The object is to propel an 8- to 10-pound pumpkin as far as possible. Steve Young of Hopewell, Illinois, set the 1998 world record of 4026.32 feet. Suppose you build a machine that fires the pumpkin so that it is at a height of 124 feet after one second, 272 feet after three seconds, and the height at eight seconds is 82 feet. Refer to the formula in exercise 7 to find the acceleration, the initial velocity, and the initial height of the pumpkin.
I find it strange that the teacher wants me to do a physics exercise when I'm working on Pre-Calculus, and moreso that he didn't specify that I would have to go back to an exercise he didn't say had to be done in this lesson, but for the sake of having more resources, this is what exercise 7 says:
The height of an object that is thrown upward with a constant acceleration of a feet per second per second (I swear to God it's written twice in the book) is given by the equation
s = 1/2at^2 + Vot + So
The height is s feet, t represents the time in seconds, Vo is the initial velocity in feet per second, and So is the initial height in feet. Find the acceleration, the initial velocity, and the initial height if the initial height at 1 second is 75 feet, the height at 2.5 seconds is 75 feet, and the height at 4 seconds is 3 feet.
Thank you for taking the time to look at this.
Gosu_Engineer
Smash Ace
I need help with a physics question, I don't know where to start.
Each year, the Punkin' Chunkin' contest is held in Lewes, Delaware. The object is to propel an 8- to 10-pound pumpkin as far as possible. Steve Young of Hopewell, Illinois, set the 1998 world record of 4026.32 feet. Suppose you build a machine that fires the pumpkin so that it is at a height of 124 feet after one second, 272 feet after three seconds, and the height at eight seconds is 82 feet. Refer to the formula in exercise 7 to find the acceleration, the initial velocity, and the initial height of the pumpkin.
I find it strange that the teacher wants me to do a physics exercise when I'm working on Pre-Calculus, and moreso that he didn't specify that I would have to go back to an exercise he didn't say had to be done in this lesson, but for the sake of having more resources, this is what exercise 7 says:
The height of an object that is thrown upward with a constant acceleration of a feet per second per second (I swear to God it's written twice in the book) is given by the equation
s = 1/2at^2 + Vot + So
The height is s feet, t represents the time in seconds, Vo is the initial velocity in feet per second, and So is the initial height in feet. Find the acceleration, the initial velocity, and the initial height if the initial height at 1 second is 75 feet, the height at 2.5 seconds is 75 feet, and the height at 4 seconds is 3 feet.
Thank you for taking the time to look at this.
The idea is to separate the trajectory into horizontal and vertical components. The horizontal component isn't really relevant. For the vertical component there is an initial velocity upward because these are generally fired at an angle upward to increase total horizontal distance. Now you use the values they give you; you should have three variables left when you plug in numbers but you have three equations. It becomes a system of equations and you solve the system to find the variables. No calculus is involved.
For the record "feet per second per second" is correct. Acceleration in Cartesian coordinates have units of (distance)/(time*time)
Kinzer
Mammy
Time multiplied by time, otherwise time squared... Yeah makes sense.
Thank you, I'll see if I can figure this out on my own later. Even if I can't, I'll be going to campus tomorrow and I'll see if I can have the teacher break it down for me. I just needed some kind of a lead.
Thank you, I'll see if I can figure this out on my own later. Even if I can't, I'll be going to campus tomorrow and I'll see if I can have the teacher break it down for me. I just needed some kind of a lead.
Dark Ryu
Smash Ace
Hi, I need help with this problem. I know it may really be easy for you guys so don't laugh.
We kept track of the number of trick-or-treaters coming to our door on Halloween through the past 20 years. The average is 33.79 visitors per Halloween. How many more trick-or-treaters will need to show up at our house this year so that the average increases to 34? In your opinion, is it likely this will occur?
We kept track of the number of trick-or-treaters coming to our door on Halloween through the past 20 years. The average is 33.79 visitors per Halloween. How many more trick-or-treaters will need to show up at our house this year so that the average increases to 34? In your opinion, is it likely this will occur?
Jane
Smash Hero
holy **** this thread is amazing. subscribing
MintyFlesh
Smash Ace
- Joined
- Jul 30, 2010
- Messages
- 577
I'm not very good at math so hopefully you guys can help =P
Write the equation of the locus of points in a plane such that the difference of the distances from (-2,5) and (4,5) is 4
Thanks!
Write the equation of the locus of points in a plane such that the difference of the distances from (-2,5) and (4,5) is 4
Thanks!
Gosu_Engineer
Smash Ace
I'm not very good at math so hopefully you guys can help =P
Write the equation of the locus of points in a plane such that the difference of the distances from (-2,5) and (4,5) is 4
Thanks!
Use the distance formula: from (a, b) to (c, d) the distance D = sqrt[(c-a)^2 + (d-b)^2]
So the problem ask for a fixed difference in distances from some arbitrary point (x, y).
|sqrt[(x-(-2))^2 + (y-5)^2] - sqrt[(x-4)^2 + (y-5)^2]|.
All the points (x, y) that satisfy the conditions are where this equation is equal to 4. Note that it is in absolute values since distance is not negative
Frame Perfect
Smash Journeyman
no .
Jane
Smash Hero
the problem is asking to write an equation, not to solve it
Gosu_Engineer
Smash Ace
That's not very helpful. Please give more feedback as to why my reasoning is wrongno .
the problem is asking to write an equation, not to solve it
|sqrt[(x-(-2))^2 + (y-5)^2] - sqrt[(x-4)^2 + (y-5)^2]| = 4|sqrt[(x-(-2))^2 + (y-5)^2] - sqrt[(x-4)^2 + (y-5)^2]|.
All the points (x, y) that satisfy the conditions are where this equation is equal to 4. Note that it is in absolute values since distance is not negative
I thought that was implicit through my wording. Again this is just what I figure. If you have something different, please by all means argue against my answer
Kason Birdman
Smash Champion
does 300 000/ 5.0 x 10^18 = 0.00000000000006 ?
thats 14 zeros in total btw.. 13 after the decimal.. 15 digits altogether.
im just freaking out cause it doesnt feel right.
and can that also be written as 0.6 x 10^-13?
thats 14 zeros in total btw.. 13 after the decimal.. 15 digits altogether.
im just freaking out cause it doesnt feel right.
and can that also be written as 0.6 x 10^-13?
yes and no. 3 E5/ 5 E 18 = .6 E-13 = 6 E -14.does 300 000/ 5.0 x 10^18 = 0.00000000000006 ?
thats 14 zeros in total btw.. 13 after the decimal.. 15 digits altogether.
im just freaking out cause it doesnt feel right.
and can that also be written as 0.6 x 10^-13?
jaswa
Smash Journeyman
If it doesn't feel right, conver everything to something similar to see if it looks about right. In this case I'd turn everything into having one number to the left of the decimal point then multiplied by a power of ten. Also I'm assuming you meant 300 000/ (5.0 x 10^18)does 300 000/ 5.0 x 10^18 = 0.00000000000006 ?
thats 14 zeros in total btw.. 13 after the decimal.. 15 digits altogether.
im just freaking out cause it doesnt feel right.
and can that also be written as 0.6 x 10^-13?
So 300 000 = 3.0 x 10^5 or 3E5 (this is how we write it on computers to make things easier)
Divided by 5.0 x 10^18 or 5E18
If you know your indice laws when you multiply you add the powers, and subtract for dividing. So ignoring the 3.0 and 5.0:
(10^5)/(10^18)=10^(5-18)=10^-13
So now you have a ballpark figure to see if you answer matches up with 'what is expected.'
Kason Birdman
Smash Champion
Hey thanks a lot :D
My physics assignment is due tomorow and that was the only question I was really iffy on.. and theres this other one about lighting and thunder blah blah... but I think I got that one
My physics assignment is due tomorow and that was the only question I was really iffy on.. and theres this other one about lighting and thunder blah blah... but I think I got that one
MintyFlesh
Smash Ace
- Joined
- Jul 30, 2010
- Messages
- 577
I ended up finding it, turns out it was a hyperbola equation, where the two points were foci, 4 is the length of major axis, so it ended up being:
(x-1)^2 over 4 - (y-5)^2 over 5 = 1
(x-1)^2 over 4 - (y-5)^2 over 5 = 1
Corpsecreate
Smash Lord
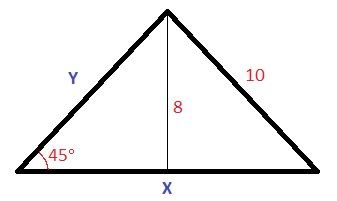
DIAGRAM IS NOT TO SCALE INTENTIONALLY!!
1. Find the value of Y as an exact value.
2. Find the value of X as an exact value.
Now replace the value of 8 with the variable H and the value of 10 with the variable L.
3. Find the maximum valid value of L.
4. Find the value of L in terms of H so that X is equal to Y.
For the record I know how to do this question, I was just bored so I created it
MintyFlesh
Smash Ace
- Joined
- Jul 30, 2010
- Messages
- 577
I have no idea how to approach this question, any ideas are very welcome 
Write the equation of the circle described.
Passes through (-2,1) (-1/2,5/2), and (-2,4)

Write the equation of the circle described.
Passes through (-2,1) (-1/2,5/2), and (-2,4)
Velox
Smash Ace
(x + 2)^2 + (y - 5/2)^2 = (3/2)^2
I drew the points on a graph and looked at them. Now, it's not necessary that the center of the circle be between the first and last points that you gave me (at first glance one might think that was the case blindly), but it actually turns out that that is the case in this case. I know that because a circle is the locus of all points equidistant from a center point. You will notice that all three of the points are (3/2) units away from the point (-2, 5/2). Thus you get the equation above.
Also, if you're wondering why that question was so weird, it's because your teacher is probably looking for you to recognize the general principles of geometry (IE. the definition of a circle is the locus of all points equidistant from some center point.) This idea of generalizing geometry is necessary in more advanced math when you might want to describe a circle in some kind of curved or unusual space. Let's say you live in a 2-dimensional world, but it's not just some flat plane, but say the surface of a sphere. If your reality is completely confined to the surface of the sphere (you live in a 2D world and can't fathom 3D), you could tell you were living in a 2D world by constructing a circle (using the GENERAL principle of a circle, equidistant and all that other stuff that I said was important..) Let's say you construct a circle and it is centered at the north pole, and you take the equidistant "circumference" of points to be those of the equator, then you've constructed a perfectly legitimate circle, but it no longer obeys D = 2PI*radius! In fact 2PI would be slightly smaller in this case. So being quite general about your geometry is important.
Also, if you're interested we can tell that we're living in a curved space (our 3 dimensional space is curved) in much the same way using somewhat similar principles. Mass curves it, and the effect is very real.
I drew the points on a graph and looked at them. Now, it's not necessary that the center of the circle be between the first and last points that you gave me (at first glance one might think that was the case blindly), but it actually turns out that that is the case in this case. I know that because a circle is the locus of all points equidistant from a center point. You will notice that all three of the points are (3/2) units away from the point (-2, 5/2). Thus you get the equation above.
Also, if you're wondering why that question was so weird, it's because your teacher is probably looking for you to recognize the general principles of geometry (IE. the definition of a circle is the locus of all points equidistant from some center point.) This idea of generalizing geometry is necessary in more advanced math when you might want to describe a circle in some kind of curved or unusual space. Let's say you live in a 2-dimensional world, but it's not just some flat plane, but say the surface of a sphere. If your reality is completely confined to the surface of the sphere (you live in a 2D world and can't fathom 3D), you could tell you were living in a 2D world by constructing a circle (using the GENERAL principle of a circle, equidistant and all that other stuff that I said was important..) Let's say you construct a circle and it is centered at the north pole, and you take the equidistant "circumference" of points to be those of the equator, then you've constructed a perfectly legitimate circle, but it no longer obeys D = 2PI*radius! In fact 2PI would be slightly smaller in this case. So being quite general about your geometry is important.
Also, if you're interested we can tell that we're living in a curved space (our 3 dimensional space is curved) in much the same way using somewhat similar principles. Mass curves it, and the effect is very real.
Corpsecreate
Smash Lord
Well its nice you have both points of the same X value.I have no idea how to approach this question, any ideas are very welcome
Write the equation of the circle described.
Passes through (-2,1) (-1/2,5/2), and (-2,4)
Equation of a circle: (X-A)^2 + (Y-B)^2 = R^2
A = X coordinate of the centre of the circle.
B = Y coordinate of the centre of the circle.
R = Radius.
So we have straight away:
(-2-A)^2 + (4-B)^2 = R^2
(-2-A)^2 + (1-B)^2 = R^2
Therefore: (1-B)^2 = (4-B)^2
B^2-2B+1 = B^2 - 8B + 16
1-2B = 16-8B
6B = 15
B = 15/6 or 5/2.
So you know the Y coordinate of the centre of your circle is 5/2. From there we can look at your second point and use the value we just got.
(-1/2,5/2)
(-1/2-A)^2 + (5/2-5/2)^2 = R^2
(-2-A)^2 + (1-5/2)^2 = R^2
(-1/2-A)^2 = (-2-A)^2 + 9/4
A^2 + A + 1/4 = A^2 + 4A + 25/4
A = 4A + 6
-3A = 6
A = -2
Ok now for R...
R^2 = (-1/2+2)^2
R = 3/2
Equation is: (X+2)^2 + (Y-5/2)^2 = (3/2)^2
MintyFlesh
Smash Ace
- Joined
- Jul 30, 2010
- Messages
- 577
Corpse/Velox, ty so much. I never would have thought of that on my own
KosukeKGA
Smash Champion
Trigonometry Problem
Hi, all. I need help because I cannot work with problems with no numbers...Just can't.
Suppose that there are two circles (a big one and small one) touching each other as so:
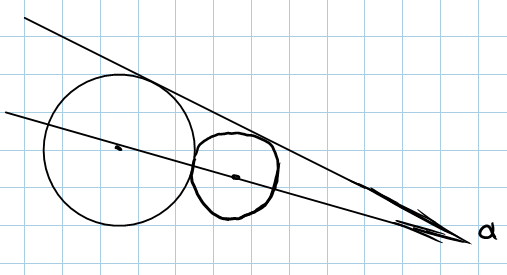
There is a line that is tangent to both circles (L1) and a line that goes through the center of both circles (L2). The angle made between L1 and L2 is alpha.
If the big circle has radians R and the small circle has radius r, find R/r in terms of alpha.
This has been bothering me for the past few hours or so. I've tried looking through my textbook and webnotes and no dice. =[
Hi, all. I need help because I cannot work with problems with no numbers...Just can't.
Suppose that there are two circles (a big one and small one) touching each other as so:

There is a line that is tangent to both circles (L1) and a line that goes through the center of both circles (L2). The angle made between L1 and L2 is alpha.
If the big circle has radians R and the small circle has radius r, find R/r in terms of alpha.
This has been bothering me for the past few hours or so. I've tried looking through my textbook and webnotes and no dice. =[
forward
Smash Champion
This problem looks fun Kosuke, I'm working on it... don't know if I will get it though.
forward
Smash Champion
Not sure if this is right but here it goes
My answer is R/r = 1/(1-tan alph)
I assumed that when you said the big circle has radians R you meant that it has radius R. A circle has 2pi radians...
I split this up into two triangles by connecting each radius from L1 to L2. This creates two 90 degree triangles and you can now use trig functions to solve.
Lets call the triangle made from the little circle T1 and the triangle made from the big circle T2. In T1, we have tan alph = r/(r+a), where a is the distance along L1 from the edge of the circle to the point where it intersects with L2.
On T2, we have tan alph = R/(R+r+a). What I did here was set these two equations equal to each other and solve for a. So we have
r/(r+a)=R/(R+r+a)
Rr + r^2 + ra = Rr + Ra
r^2 = Ra - ra
r^2 = a(R-r)
r^2/(R-r) = a
Now that we have a, we can plug it back into either of the tan alpha formulas, I did the tan for T1.
Tan alpha = r/(r+ ...
This is too much to write on here. Just plug in that a value, do some algebra to get R/r, and you got it.
My answer is R/r = 1/(1-tan alph)
I assumed that when you said the big circle has radians R you meant that it has radius R. A circle has 2pi radians...
I split this up into two triangles by connecting each radius from L1 to L2. This creates two 90 degree triangles and you can now use trig functions to solve.
Lets call the triangle made from the little circle T1 and the triangle made from the big circle T2. In T1, we have tan alph = r/(r+a), where a is the distance along L1 from the edge of the circle to the point where it intersects with L2.
On T2, we have tan alph = R/(R+r+a). What I did here was set these two equations equal to each other and solve for a. So we have
r/(r+a)=R/(R+r+a)
Rr + r^2 + ra = Rr + Ra
r^2 = Ra - ra
r^2 = a(R-r)
r^2/(R-r) = a
Now that we have a, we can plug it back into either of the tan alpha formulas, I did the tan for T1.
Tan alpha = r/(r+ ...
This is too much to write on here. Just plug in that a value, do some algebra to get R/r, and you got it.
Jane
Smash Hero
ok simple question. i thought i knew how to do this but i get the wrong answer X_x.
find the x-intercepts of y=2x^2+x-6
im getting 6 and -1/2 but its wrong D: i get the correct vertex and y-intercept... but not the x-ints. what am i doing wrong or how do i do it correctly?
find the x-intercepts of y=2x^2+x-6
im getting 6 and -1/2 but its wrong D: i get the correct vertex and y-intercept... but not the x-ints. what am i doing wrong or how do i do it correctly?
KosukeKGA
Smash Champion
^
That problem was the only one that had me going for a while on my homework...It makes sense to me now w/ your explanation. :]
Thanks, Sean!
That problem was the only one that had me going for a while on my homework...It makes sense to me now w/ your explanation. :]
Thanks, Sean!
kidneybeans
Smash Apprentice
The x-intercept is when it crosses the x-axis. An x-intercept should always have what corresponding y-value?ok simple question. i thought i knew how to do this but i get the wrong answer X_x.
find the x-intercepts of y=2x^2+x-6
im getting 6 and -1/2 but its wrong D: i get the correct vertex and y-intercept... but not the x-ints. what am i doing wrong or how do i do it correctly?
Hence you want the x values such that....?
Corpsecreate
Smash Lord
x-intercepts occur when y is 0.ok simple question. i thought i knew how to do this but i get the wrong answer X_x.
find the x-intercepts of y=2x^2+x-6
im getting 6 and -1/2 but its wrong D: i get the correct vertex and y-intercept... but not the x-ints. what am i doing wrong or how do i do it correctly?
2x^2 + x - 6 = 0
Use the quadratic formula: x = (-b +- sqrt (b^2 - 4ac ) )/2a
x = (-1+7)/4
x = (-1-7)/4
x = 3/2 , -2
Jane
Smash Hero
oh right. i tried using the factoring method to get the answer. i forgot that sometimes that doesnt work. i should have used the quadratic formula. thanks!
Corpsecreate
Smash Lord
The factoring method does work its just harder to spot this time because of the 2x^2
(2x+4)(x-3/2) = 2x^2 + x - 6
(2x+4)(x-3/2) = 2x^2 + x - 6
Jane
Smash Hero
.....****. lol, youre right. i was just making a ******** mistake when attempting to factor and somehow it "looked" like it was the correct way.
Tee ay eye
Smash Hero
can someone explain to me how the distance formula is related to the arc length formula?
my textbook has something demonstrating how they used the arc length formula to find the distance between (X1, Y1) and (X2, Y2), but i don't really get why.
my textbook has something demonstrating how they used the arc length formula to find the distance between (X1, Y1) and (X2, Y2), but i don't really get why.
Sasha
Smash Journeyman
It's difficult to explain without me drawing up some formulas, so hopefully the wikipedia explanation will work well enough.
http://en.wikipedia.org/wiki/Arc_length#Finding_arc_lengths_by_integrating
In short: the arc length formula is derived by looking at the distance formula (which is essentially a result of the Pythagorean Theorem) and integrating that formula over the distance from X1 to X2 while looking at the change in Y values from Y1 to Y2 given by the original function y=f(x).
Let me know if you'd like me to explain it further, or if this is at all what you were looking for.
http://en.wikipedia.org/wiki/Arc_length#Finding_arc_lengths_by_integrating
In short: the arc length formula is derived by looking at the distance formula (which is essentially a result of the Pythagorean Theorem) and integrating that formula over the distance from X1 to X2 while looking at the change in Y values from Y1 to Y2 given by the original function y=f(x).
Let me know if you'd like me to explain it further, or if this is at all what you were looking for.
