With the ever nearing release date of brawl, the smash community will find itself at an important point in its future. We will as a community come to a consensus on many issues as to what should and should not be included in competitive play. In addition to this, however, brawl's release gives us the opportunity to reevaluate the basic tournament mechanics that we likely take for granted. There are many highly misunderstood aspects to tournaments today that are standard and others that are ignored for poor reasons. This article will explore those mechanics to better aid tournament directors in making decisions.
To begin, let's define some terms that we will be using throughout this discussion.
- Accuracy: The accuracy of a tournament is the quality that players should place according to their skill. (Skill being defined in a moment) But the gist is that the "best" player should place 1st, the 3rd "best" person should place 3rd, etc…
- Fairness A tournament system that does not give advantages to any players rather than others is called Fair.
We have all been to a tournament where a relatively unskilled player advances far through a bracket by way of not having to play tough opponents. Conversely, we have all seen highly skilled players knocked out of a tournament early by having to play other highly skilled players immediately. Both of these situations are "unfair".
- Number of games played Self explanatory: The total number of matches played by all participants in a tournament.
Playing is fun, and we would like to be able to squeeze in as many games as possible. Tournaments where you get to play a single match and then are eliminated are not fun. So this value would like to be maximized.
- Total amount of tournament time.: Related to Number of Matches Played, this is the actual amount of time it takes to run the tournament.
Tournaments cannot take a week to finish; they must be able to be completed in a reasonable amount of time. Thus this number should be minimized.
- Skill: An underlying approximation to how "good" you are. This is a single numerical value which is used to represent how adept at the game as a whole someone is.
- Performance: This is a positive or negative value depending on how well you are playing during a particular match. It is notw how "good" you are in general, but how well you are playing relative to your average today.
If you SD twice at zero percent in a match, you would have a very low performance for that match. If you zero-to-death your opponent flawlessly several times in match, that would be an indication of you having a high performance value for that match.
- Consistency: Performance values for a player are normally distributed across matches. The standard deviation of this set of values is called the player's consistency.
- Seed: A pre-ranking of players in a tournament according to their expected placement. This should essentially be a ranking of players' believed skill values. Note that lower seeds indicate high skill. (IE: seed #1 goes to the highest skill, etc...)
- Entertainment: (of a match) A match is called entertaining if it is between two players who have similar skill. (As defined above) Also, the higher the combined skills of the players, the higher the entertainment value. Entertainment of matches should be maximized.
- Upset: An upset is defined as when a player of lower skill beats a player of higher skill, typically due to some combination of the higher skilled player having a poor performance and the lower skilled player having a high performance.
A "perceived" upset occurs when a lower seed loses to a higher seed due to inaccuracy of the seeds. IE: If a "no name player" is actually highly skilled, he may receive a high seed and appear to upset lower seeded players.
Seeding
Seeding is a very important (and often ignored) aspect of running a successful tournament. All professional sports leagues (NFL, NBA, MLG, etc...) use seeding in their brackets, and there's no reason for you not to. Let's move on to the details of why.
Accuracy: Accuracy is increased if seeding is used. Players of high skill will be seeded away from each other initially, so that when they eliminate each other, it will be at near the end of the tournament as opposed to the beginning. This will help to ensure that high skilled players place highly and lower skilled players place lowly.
Fairness: Brackets seeded to ranking are often criticized for their unfairness. It is believed commonly that seeding favors higher ranked players by giving them "easier" opponents. This misconception is typically brought about by the fact that the first matchup the 1st seed plays is against the lowest seed. So players often complain that that person gets "an easier bracket".
But here's the problem: I've been sort of lying to you up until now, Accuracy and Fairness are actually the same thing. In a tournament, if you have perfect Accuracy, everyone will place exactly according to their skill values if no upsets occur. (IE: If you're the best, you get 1st, 4th best, you get 4th place.) How can this possibly be called unfair? Indeed it is perfectly fair!
A seeded bracket ensures the following: If you perform according to your seed (beating everyone worse than you, losing to everyone better than you), you will place as your seed indicates. This is of course optimally fair.
Example: If you are the 7th best person in the tournament, no upsets occur, and you place 3rd in the tournament, then the bracket was unfair to you! You placed more highly than you should have. The only way someone should be able to place higher than what their seed indicates is by upsetting players of higher skill.
How to seed? Ranked seeding should always be done in the following pattern: (given for 16 players)
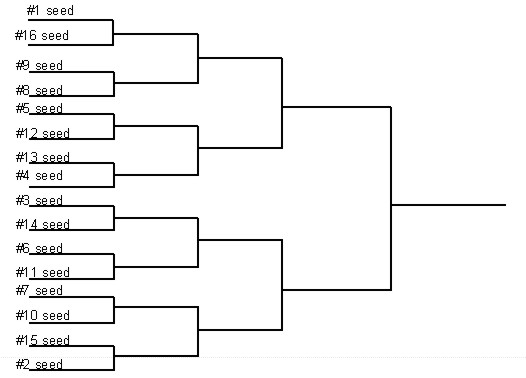
This pattern is chosen for a specific reason: it guarantees an even distribution of skill at all levels except the final. (Where it is impossible) You should notice that all first round matchups a have players adding seeds to 17. This means that each half of the bracket has total ranking points of 68. You can see that there is no "preferable" place to be on the bracket at any particular level, making the bracket perfectly fair. The skill values for every area sum to the same values. In round two, for example, every matchup sums to 9.
Entertainment: Seeding by rank ensures that the higher skilled players will play each other, thus entertainment is increased. In general, the entertainment of matches in a bracket increase as the tournament progresses.
Double Elimination Bracket
Double elimination has several effects on a tournament, which can be summarized as such:
Number of matches: Making a tournament double elimination doubles the number of matches that need to be played.
Time To Complete: Adding double elimination to a tournament will more than double the total time to complete it. (Read the next section on Concurrency for an explanation as to why adding double elimination more than doubles the total tournament time.)
Accuracy: Double elimination will increase the accuracy of a tournament by increasing the number of games a player must win in order to upset better players. IE: If the probability of an upset is 1/4, the probability of it happening twice consecutively is 1/16! Playing more games makes it more unlikely that an upset will occur.
All Brackets
Accuracy In the real world, (due to seeding inaccuracies) brackets tend to be increasingly accurate at the top of the placings, and less accurate at the bottom of the placings.
Number of matches: This is really fairly simple. Think of it this way: each game played causes a player to get a loss. The tournament ends when all but on player has 2 losses. The number of games in the tournament must then be the number of losses each player can have times the number of people in the tournament:
Single Elim= n sets to be played
Double Elim = 2n sets to be played
Time To Complete: (Concurrency) We have all been to a tournament where everything is moving quite smoothly during the entire process right up until the final few matches. The end of a tournament almost always tends to drag on long past everyone's expectations. (sometimes well into the morning hours) Why is this?
It is because bracketed tournaments rely on Concurrency. That is: the fact that some matches cannot be played until certain other ones have finished. It seems obvious, yes? The finals cannot be played until the semi-finals have finished, after all. And this phenomenon has a profound delaying effect on bracketed tournaments.
This makes the formula a bit more complex, but don't be scared off. Just use a calculator, and let it do the hard work.
[ 15kn/TV ] + 10log2(n)
An important thing to note is that the second part does not have a TV variable in it. This is intentional, because it represents the second half of the rounds in a bracketed tournament. These matches must be played one after another, and having additional TV's doesn't help to speed it up.
Also of note is that the second part of the formula runs on a higher order than the first, that means that for large tournaments: even though you finish 75% of the matches, you're still less than half of the way done in terms of time. This is why tournaments frequently run over time at the end. They think "well, we're almost done with the matches" when really you're only about half way done.
Round Robin Tournaments
Round robin is an alternate method of running a tournament instead of using a bracket. In a nutshell, Round Robin involves each participant to play every other participant. We will now explore the various pros and cons to this alternate tournament scheme.
-Accuracy: In general, round robin tournaments are more accurate than brackets of any variety. The reason is obvious: every possible matchup is played. You have the maximum amount of data from which to declare a winner instead of just a subset of that data.
-Fairness: Round Robins are also perfectly fair. Every player plays exactly the same people, so this is apparent. In comparison, seeded brackets are considered fair because they offer each player equivalent matchups. Round Robin goes one step further and offers identical matchups.
-Entertainment: Since every matchup is played, every appealing match can be viewed. However, the average entertainment value of a Round Robin match is rather low. This is because the majority of the games being played are not between two closely and highly skilled players. In comparison, brackets tend to eliminate out the lower skilled players, quickly leaving the majority of matches played entertaining.
-Number of Games Played: This is the very famous “Handshake Problem”. Long story short, the number of sets in a round robin are [n(n-1)/2]. Which is a lot compared to a double elimination bracket with only 2n games.(Where n = number of participants)
-Time to Complete Tournament:
This is where round robin fails. Simply put, they take too long to finish for any more than a dozen or so people.
n(n-1)/2 sets
5n(n-1)/4 matches (Averaging 2.5 matches / set)
5n(n-1) minutes (Average of 4 minutes / match)
5kn(n-1) minutes (Scaled to consider an efficiency coefficient, k)
5kn(n-1)/TV minutes (Scaled to consider multiple TV setups)
Total time to run a Round Robin tournament formula: 5kn(n-1)/TV
Where:
n = Number of participants
k = efficiency coefficient that describes how efficiently you ran your tournament. (as little wasted time as possible)ost to tell me how long it took from start to finish, how many people you had
TV = The number of total setups for the tournament. (TV’s + Cubes in the case of smash)
Note that the formula gives you the total time in minutes! You have to convert to hours + minutes. (IE you might get 190, which means 3 hours, 10 minutes)
I have found so far that 1 is not a bad starting point for k. But if you run a round robin, please post saying:
1) How long it took from start to finish.
2) How many total setups you had.
3) How many people participated.
I would very much like to get a good empirical value for k. Also, it might be fun to try and compare k values for tournament efficiency bragging rights!
- Intangible: Round Robins have the flaw that it is always possible that you get a tie. In fact, it is possible that everyone in the tournament tie for first and last simultaneously! In comparison, brackets have the advantage of always being able to declare a clean cut winner.
Pools
Pools are a tournament mechanic used to form a hybrid of both round robins and brackets. What is done is all players are separated into groups called Pools. Each pool runs a round robin tournament within each other, and then the top X from each pool will move on to a regular bracket. (Or more rounds of pools, in some cases)
Note that Pools are typically only run in a sufficiently large tournament, not smaller ones.
Accuracy Pools drastically help to increase the accuracy of a large tournament. This is because the task of accurately seeding every player is not practical. With pools, one needs not seed every player, but rather only about 1 or two per pool, which is much more manageable.
The other effect is: self-seeding. Pools are a good way of matching player up against one another to detect any obvious and egregious oversights in the seeding process. For example, if an unknown player is actually highly skilled, he will have the opportunity to give himself a high bracket seed by placing well in pools. The seed going into the pools does not matter as much.
Time to Complete:
Let:
a = number of pools
b = number of people per pool
n = total number of people
k = efficiency coefficient
TV = number of TV's used
5kn(n-1) /TV (Round Robin formula)
5kb(b-1) /TV (Pool of b people)
a * 5kb(b-1) /TV("a" pools of b people each)
5kn(b-1) /TV (simplified)
5kn(b-1)/ TV
This is the formula to compute how long it will take to complete "a" number of pools, with total participants on n. As you would have guessed, it looks remarkably similar to the Round Robin formula.
Other things to consider:
Continuation Sets: A continuation set is a way of handling rematches in a double elimination bracket. Most smashers recognize it by the way MLG handles rematches. I’m not sure why, but the general opinion of this is overwhelmingly negative. The fact is that having a continuation set is a better method than having each set handled separately.
The reason is that the winner is guaranteed to have won more games over his opponent. I’ll use an example here from an actual tournament that took place here in Arizona not long ago.
-Player 1 wins the winners finals set 3-1
-Player 2 comes back into the championship finals and wins the second set 3-2
-Player 2 then wins another set 3-2.
-Player 2 wins the tournament.
But you can see that they both won 7 games! Player 2 is awarded the victory in the tournament because of the order in which he won the games, not how many games he won, which should be the case. A continuation set essentially says “You have to win more games over your opponent in order to beat them” which is perfectly reasonable.
Thanks for reading! I would like to keep adding to this article, so please let me know if there is anything that needs adding, removing, or modifying. I’d love to hear what you have to say!
Coming soon:
-Analysis of pools.
-AltF4
