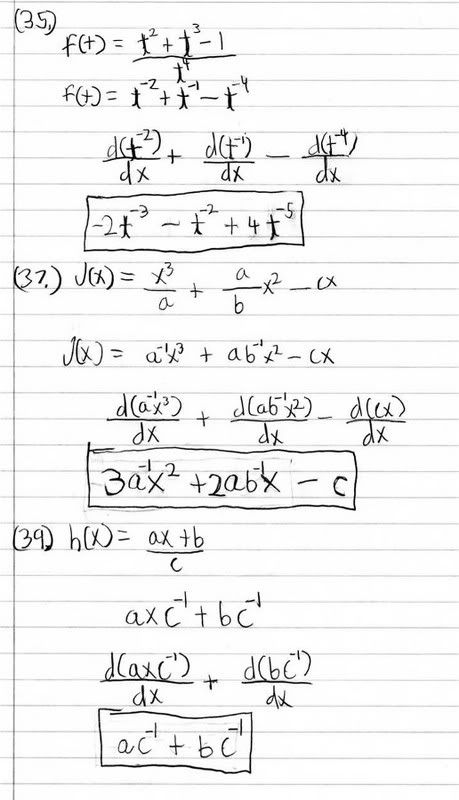Need Math Help?

[AltF4]

35) the last term doesn't reduce to (t^-3) it's (t^-4). You subtract the exponents, and when there's no 't' that means an exponent of zero. So zero minus four is negative four.

37) You're doing the derivative with respect to x. (d/dx) That means when you do the derivative, treat any letters other than x like a constant. Don't take the derivative of a, just leave it as if it were the number 4. Besides, even if you were to do the derivative for both variables, that's not how you do it. You'd have to do product rule.

38) Same thing. When you're doing the derivative with respect to x, pretend that every other letter is just a regular old number. So that means the derivative with respect to x of (b/c) is zero.

 

[Varuna]

Hey thanks alot! Is this any better?

 

[AltF4]

All good except the second term of #39). When you take the derivative of a constant, you get zero.

 

[Lixivium]

Are those 't's or 'x's in 35?

d/dx(x) = 1

but

d/dx(t) = 0

 

[AltF4]

Oh, ha. I didn't even notice that. He probably meant to write d/dt. Since it's a function of t. You just get so used to writing d/dx.

 

[Zarelid]

weird seein Goldshadow and TGM postin in the same thread lolz -=rememberz old dayz=-

 

[GoldShadow]

Whoa, I didn't even see TGM's post! That is pretty cool. You know what's weirder? Seeing me, TGM and Zarelid posting in the same thread...


btw AltF4 (or somebody), could you briefly just explain the idea of 'determinants'? It was brought up in physics class but we did not really discuss it much.

 

[AltF4]

Hah. I remembered how to do determinants... but I couldn't really remember a good description of what they ARE.

It's an operation you can do to a matrix to get a value. You get a single number out of it that has a couple interesting properties. Like if you use the matrix to represent vectors, the determinant represents the volume formed by the parallelepiped the vectors make. (a multi-dimensional parallelogram)

 

[cF=)]

I'll just add something to what AltF4 said.

In physics (especially in electricity), you'll frequently solve equations with 2 or 3 variables. A swiss mathematician named Gabriel Cramer invented a quick way to find the identity of these variables using a square matrix and determinant.

Let's take a random equations system in exemple:

(1) ax + by = e
(2) cx + dy = f

We then put these numbers in a matrix:

Now, in a 2x2 matrix, the determinant will be given by the formula ad - cb. Afterward, to find the value of x, you switch the first column of your matrix by the result of your 2 equations and you divide by the determinant. To find the value of y, you switch the second row and divide by the determinant :

Finding the det. for a matrix over 2x2 is different, so I won't venture myself into that over the internet.

EDIT: I hate drawing with a mouse

 

[Hyrulean21]

2x2 matrix is actually easier than that. Say for example you have matrix

A B
C D

the determinant is AD-BC.

3x3 is a pain, and there are several ways to do them, depending on what you prefer.

Ok, time for some Differential Equations. My professor likes to skip a lot of steps in the lectures, so I didnt' quite follow all of what he did with this.

Find the general solution of the differential equation:

y'+y = t*e^(-t) +1

The answer the back of the book has is y = ce^(-t) + 1 + t^2*e^(-t)/2

While my answer is y = 1 + t^2*e^(-t)/2


I can't find where I lost that extra term...

 

[Lixivium]

Ok, time for some Differential Equations. My professor likes to skip a lot of steps in the lectures, so I didnt' quite follow all of what he did with this.

Find the general solution of the differential equation:

y'+y = t*e^(-t) +1

The answer the back of the book has is y = ce^(-t) + 1 + t^2*e^(-t)/2

While my answer is y = 1 + t^2*e^(-t)/2


I can't find where I lost that extra term...

I get what your book says. You are using the integrating factor right?

y' + P(t)*y = Q(t)
P(t) = 1
Q(t) = t*e^(-t) + 1

IF = e^(int(1 dt))
IF = e^(t)

The general solution is then:

y = 1/(IF) * int( Q(t) * IF dt )
= e^(-t) * int( (t*e^(-t) + 1) * (e^t) dt)
= e^(-t) * int((t + e^t) dt)
= e^(-t) * (1/2*t^2 + e^t +C2)
= 1/2*t^2*e^(-t) + 1 + C*e^(-t)

You forgot the constant you get from integrating (t + e^t) dt. I don't what happens to that first constant from the integrating factor though.

 

[Haruno Kotetsu]

dude im in high school and dont know long division

 

[cF=)]

Anybody here knows how to do square roots without a calculator ?

 

[Doraki]

Find the general solution of the differential equation:

y'+y = t*e^(-t) +1

The answer the back of the book has is y = ce^(-t) + 1 + t^2*e^(-t)/2

While my answer is y = 1 + t^2*e^(-t)/2.

What you did is find only a single solution f(t).
Most of the time, there'll be a lot of other solutions.
But this is a linear equation :
If there is another solution g, you have f'(t) + f(t) - g'(t) - g(t) = t.e^(-t)+1 - t.e^(-t)-1 = 0

Thus (f-g)'(t) + (f-g) (t)= 0
So the acceptable functions are the one whose difference with f satisfies y' + y = 0

The solutions to y' + y = 0 are the C * e^(-t), thus the complete set of solutions of the original equation is the functions t -> f(t) + C * e^(-t).

Anybody here knows how to do square roots without a calculator ?

There is a way, and it really gets a hassle when you're getting a lot of digits.
Unless you're working with the square of a 2-digit or maybe 3-digit integer, I advise you get a calculator.

Say you have 1156.
1156 is between 900 and 1600, which means the square root is between 30 and 40
Thus you have 1 digit of the square root, 3.
You remove 30^2 from 1156, you get 1156 - 900 = 256
now (30+x)^2 = 900 + 60x + x^2. So you'll be trying to get an x by dividing that remaining term by 60.
1156 - 900 = 256= 60 * 4 + 16
Then you get a candidate for the second digit, 4.
Then you remove 4^2 from the remaining 16, and you find 0, which means the square root is exactly 34.
You can get a negative term (when the digit obtained is big) then you get a minus sign in some of the calculations but it's no too much trouble.

You have to keep 3^2, 34^2, and all the consecutives squares in the process and in the end it can become big. And dividing by 2*34 or whatever still without a calculator isn't that easy.
This method is getting more and more accurate approximations of your square root as you get more digits.

If you know beforehand you're given the square of an integer, you can try to check for divisibility by 2,3,5,11, and reduce the problem.
One time I was playing smash and someone asked me "what's the square root of 4356 !?"
I immediately see it's divisible by 2,11, and then 3, which led to a quick answer, 66.

 

[Hyrulean21]

Yup, I found it earlier today on my own. I felt really stupid, too. Oh well, problem solved at least.

 

[B-Will]

Probably an easy question:

Find the limit as t approaches 5 (doing it algebraically):

(5t-t^2)/[(5t)^.5 - (5+4t)^.5]

I know to multiple the top and the bottom by the conjugate of the denominator.
The problem is, is that it results with the top being all complicated after foiling it and I don't know how to simplify the equation any more to be able to find the limit.

Any ideas of how to do this?

 

[cF=)]

Find the limit as t approaches 5 (doing it algebraically):

(5t-t^2)/[(5t)^.5 - (5+4t)^.5]

It's a 0/0. Use l'Hôpital's rule

EDIT: Added a picture
EDIT2: Call me on my mistake if I did one.
EDIT3: I'm sorry in advance if you have not seen derivatives yet

 

[Lixivium]

edit: Incorrect stuff, cF=) is right.

 

[cF=)]

5 - 2t
-------------------------------------
5 * .5 * t^(-.5) - .5 - 4 * .5 * (5 + 4t)^(-.5)

That's what you forgot

 

[Lixivium]

That's what you forgot

Actually, now that I look at it I mistakenly thought (5t)^(1/2) = 5(t^1/2).

You're right, but those (-1/2)'s in the first two lines threw me off. I thought you had taken a second derivative for some reason.

 

[cF=)]

You're actually right, why the **** I put (-1/2) in the first 2 lines ?

I'll correct this, thanks.

 

[I T I]

0.999... = 1?

 

[B-Will]

Hey CF. I have already taken this class; this problem was for a friend who is currently taking this class and haven't seen derivatives or anything. He is supposed to solve this problem algebraically.

You have to somehow manipulate the equation, algebraically, so that when t=5, it doesn't make the function undefined (as it does now). No shortcuts.

Your way looks good, though.

EDIT: Nevermind. I figured out how to do it. It was easier than I thought; I just thought too hard about the problem.

After multiplying the top and the bottom with the conjugate, you are left with t-5 on the bottom. This can be cancelled out by a t-5 from the top; something I overlooked for some reason. Thanks though!

 

[AltF4]

No, you can't do that B-Will. Because in the case of t=5, you're dividing by zero. Dividing zero by zero in fact. L'Hopital's rule is for that kind of case.

 

[Doraki]

Yes he can, because studying the limit is studying the function near t=5, where the simplification can take place.
I should have spotted that there would be a cancellation when I read the problem though. I was too lazy to try the conjugate thing.

 

[AltF4]

Well, it can be useful in finding the location where the problem occurs. But I guess what I mean is that you change the equation when you cancel (t-5) it's not the same equation anymore. Because it's not a legal move, math-wise. Unless you know somehow that t cannot be 5 in that problem.

 

[Doraki]

Of course t cannot be 5.

 

[B-Will]

Of course t cannot be 5.

lol, yeah. We know that t cannot be 5 so the only way to do it algebraically is by manipulating the equation so that the equation is not undefined at t=5. We are talking about what f(t) approaches as t approaches 5, not what f(t) is at t=5.

 

[AltF4]

Heh, I don't think I explained what I meant very well again perhaps. What I'm saying is that functions:

f(x) = x (x-1) / (x-1)

g(x) = x

g and f are NOT the same function. They are not equivalent. Because you're not allowed to cancel the (x-1)'s.

For the sake of finding the limit or whatever, sure you can mess with it. Because the limit at x approaches 1 in f(x) will be equal to g(1). But you can't cancel that factor then proceed onward without it and pretend that like it's still the same equation. Because it's not.

But now if f(x) happened to have the restriction (for all x > 2) put on it, then f and g would be equal to each other. With that restriction, you would be allowed to cancel the (x-1) because you know that the factor cannot be zero.

But you guys already know this, I'm just explaining myself.

 

[B-Will]

lol, yeah I know what you mean. When you are manupulating functions so they no longer has the same properties like the same domain, it is no longer equal to one each other.

 

[Varuna]

thanks in advance!

 

[Ripple]

help find the equation of the set of all points P(X,Y) that satisfy the given conditions.

P(X,Y) is 2x as far from (-8,8) as from (-2,2). the answer is X^2 +Y^2=32 if that helps, I just can't seem to solve it correctly.

P(X,Y) forms with (4,0) and (-4,0) the verticies of a right triangle with P the vertex of the right angle. answer is X^2 + y^2=16

thanks to who helps me with this

 

[Lixivium]

P(X,Y) is 2x as far from (-8,8) as from (-2,2). the answer is X^2 +Y^2=32 if that helps, I just can't seem to solve it correctly.

This is an easy one. Remember how to find the distance between 2 points: the Pythagorean theorem.

You know that

distance from (-8, 8) to (X, Y) = 2 * distance from (-2, 2) to (X, Y)

Write out the two equations for the distances, simplify as much as you can, and you should get the answer.

P(X,Y) forms with (4,0) and (-4,0) the verticies of a right triangle with P the vertex of the right angle. answer is X^2 + y^2=16

thanks to who helps me with this

This one I can't solve rigorously. It makes intuitive sense to me that a point that forms a right triangle must be somewhere along a circle with radius 4, centered at zero. Knowing that, writing the equation is easy, but I can't explain why the point has to be on that circle.

Anyone else want to try?

 

[Lixivium]

Varuna:

Your answer looks right, but you can simplify one more step:

ln(P) - ln(Po) = ln(P/Po).

You get the same thing if you divide both sides by Po before taking the natural log.

 

[shadydentist]

@ ripple

Lets call (4,0) Q and (-4,0) R

its a right triangle, so you know that QR^2 = PQ^2 + PR^2

so lets call P(x,y)

QR=8, PQ+=sqrt( (x-4) ^2 + y^2) and PR = sqrt( (x + 4)^2 +y^2)

And solve.

 

[xyouxarexuglyx2]

How important is Algebra 2 to Pre-Calculus?

 

[AltF4]

If you want to be any kind of scientist / engineer, critically important. Factory worker / garbageman, maybe not as important. Math builds upon itself, so if you don't really get a good grasp of Algebra, you're going to have a really rough road for every class ahead of it.

Wow @ other people answering questions! That's great. It's good that everyone is jumping in to help out with answers. Keep it up.

 

[Varuna]

Ok I don't even have any idea of where to start on this. Thanks a lot in advance for any help!



Find the derivative of:

2^2^X^2

 

[Doraki]

call f1(x) = x^2
then f2(x) = 2^f1(x)
and f3(x) = 2^f2(x).

You should know how to get f1'(x), then f2'(x), and then f3'(x).

 

[Lixivium]

This is a tricky one. I had to look up derivative of f(x) = 2^x myself.