3. You are standing on the deck of a freighter heading north at 5.0 km/h. You measure the wind speed and direction as 5.0 km/h [E]. What is the actual velocity? (7.1 km/h [NE]).
This one's actually a pretty easy vector addition problem! The ship is moving north at 5 km/h, so it will make it seem like wind is traveling south at 5 km/h. We'll call this a vector with coordinates
(0,-5). Then there's the real wind blowing in some unknown direction; we'll say the coordinates for this vector are
(x,y). When you add these two vectors, we get the wind velocity that is measured by someone on the ship: 5.0 km/h east. We'll say the coordinates for this vector are
(5,0). The sum looks like this:
(0,-5) + (x,y) = (5,0)
The actual wind direction's components turn out to be (5,5). Just use pythagorean theorem to get the answer:
sqrt((5)^2 + (5)^2)
, which is about 7.1 in a northeast direction.
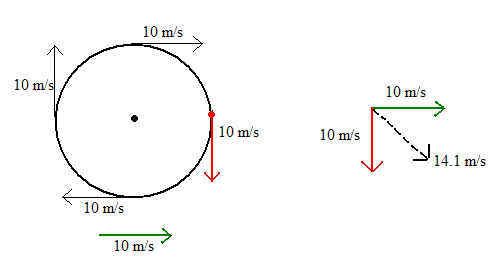
4. A wheel with a radius of 50 cm is rolling along the ground at 10 m/s [E].
a) What are the velocities of the top, bottom, front, and back points of the wheel, relative to the axle?
b) What are the velocities of those four points relative to the ground? (20 m/s [E], 0 m/s, 14 m/s [E45.0°D], and 14 m/s [E45.0°U].
If the whole thing is moving along at 10 m/s, then it means every point on the wheel is also moving at 10 m/s. If this doesn't make sense, think of it this way. The circumference of the wheel is 2π(0.5m), which is just π meters. The wheel is moving at 10 m/s, which means that in one second, the wheel has to go through (10/π) rotations (since 10 is the speed and π is the circumference). Thus, any one point on the wheel travels π meters per rotation (since that's the circumference) times 10/π rotations, which is still just 10.
For part (b), you just have to use that knowledge and add some vectors. Draw a circle. It is traveling east, so the top of the circle will be traveling directly right; coordinates of this vector are (10,0). A point at the front of the axle will be traveling straight downward; the coordinates for this vector are (0,-10). A point at the bottom will be traveling directly left; the coordinates are (-10,0). A point at the back will be traveling directly upward; its coordinates are (0,10). For each of these points, remember that the entire wheel is traveling 10 m/s east. So for each point, add (10,0) to its vector. For example, for the top, it's just (10,0) + (10,0) giving a total of
(20,0), or 20 m/s east. Repeat this for the other points on the wheel.
) but thanks for creating it, Goldshadow!
This is...high school chemistry. Not to nullify a legitimate compliment. Just pointing something out.
